Yesterday’s solution already looks facepalm worthy even though its been only 24 hours since. Hopefully today’s parsing code will be better. Let’s do this.
Day 2 - Part 1
Sample input for the first part is :
Game 1: 3 blue, 4 red; 1 red, 2 green, 6 blue; 2 green
Game 2: 1 blue, 2 green; 3 green, 4 blue, 1 red; 1 green, 1 blue
Game 3: 8 green, 6 blue, 20 red; 5 blue, 4 red, 13 green; 5 green, 1 red
Game 4: 1 green, 3 red, 6 blue; 3 green, 6 red; 3 green, 15 blue, 14 red
Game 5: 6 red, 1 blue, 3 green; 2 blue, 1 red, 2 green
The games are numbered and each game has multiple sets separated by ; with
colored cubes taken from a bag. The condition is that maximum 12 red, 13 green and 14 blue cubes are allowed. So if any set in a game exceeds this
limit, the game becomes invalid. We have to calculate the sum of id’s of valid
games. With the sample input, games 3 (20 red) and 4 (15 blue) are rejected and
sum of id’s of the remaining games is 8.
We could take a shortcut here without parsing everything, but the unknown part 2 might become harder, So it is better to just parse everything to proper data structures.
We will continue with the same image we used yesterday, which already has PetitParser loaded in it. Open a new playground get the sample input in it:
| input |
input := 'Game 1: 3 blue, 4 red; 1 red, 2 green, 6 blue; 2 green
Game 2: 1 blue, 2 green; 3 green, 4 blue, 1 red; 1 green, 1 blue
Game 3: 8 green, 6 blue, 20 red; 5 blue, 4 red, 13 green; 5 green, 1 red
Game 4: 1 green, 3 red, 6 blue; 3 green, 6 red; 3 green, 15 blue, 14 red
Game 5: 6 red, 1 blue, 3 green; 2 blue, 1 red, 2 green'.
Let’s build up our parser.
| input aColor |
"omitted"
aColor := 'red' asParser
/ 'green' asParser
/ 'blue' asParser ==> [ :c | Color named: c ] .
We are not just matching color words but also transforming the result as actual color objects:
anInteger matches and transforms an integer number:
| input aColor anInteger |
"omitted"
anInteger := #digit asParser plus token flatten ==> [ :d | d asNumber ].
aCube is just a number with a color:
| input aColor anInteger aCube |
"omitted"
aCube := anInteger , aColor trim.
trim is used to also match surrounding whitespace. aSet and aGame are
slightly more involved, but they are built incrementally with rapid feedback.
| input aColor anInteger aCube aSet aGame |
"omitted"
aSet := ((aCube , ',' asParser trim optional ==> [:c | c allButLast]) plus
, ';' asParser optional) ==> [ :set | set at: 1 ].
aGame := ('Game ' asParser, anInteger , ':' asParser)
==> [:game | game at: 2], aSet trim plus.
Unlike yesterday, we are not just matching stuff but also using transformers to
get rid of ,, ;,Game and : etc. with this the parsing is complete.
aGame matchesSkipIn: input
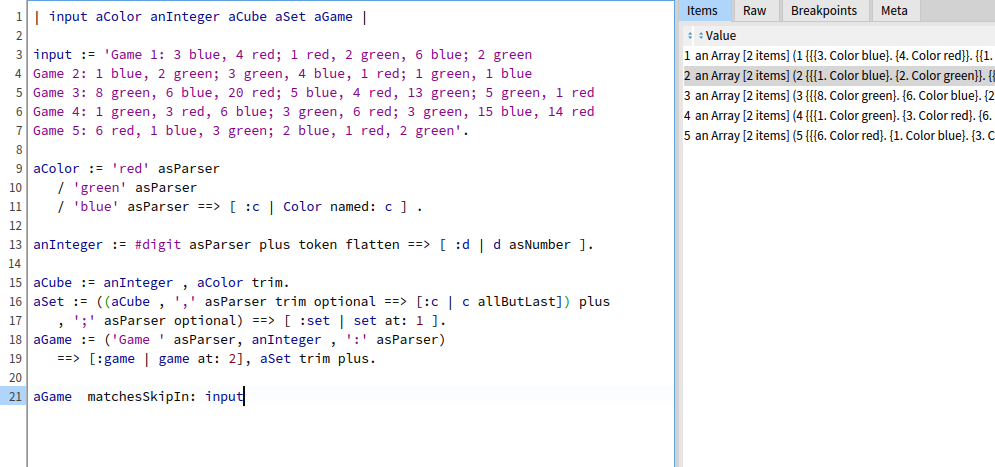
Put the parsed result in gamesCollection variable
| input aColor anInteger aCube aSet aGame gamesCollection |
"omitted"
gamesCollection := (aGame matchesSkipIn: input).
Now to solve the puzzle we need to know whats the maximum number of cubes of each color are in a game.
I defined a block function (lambda / anonymous function equivalent) which we store in another variable.
| input aColor anInteger aCube aSet aGame gamesCollection maxRGBinSingleGame |
"omitted"
maxRGBinSingleGame := [ :game |
| dict |
dict := Dictionary new.
dict at: (Color named: 'red') put: 0;
at: (Color named: 'green') put: 0;
at: (Color named: 'blue') put: 0.
(game at: 2) do: [ :each | each do: [ :c | ((dict at: (c at: 2)) > (c at:
1))
ifFalse: [ dict at: (c at: 2) put: (c at: 1) ]]].
{ (game at: 1) . dict }.
].
It basically creates a Dictionary with RGB counts at 0, then iterate on each set
and check if the RGB count is > than the local dict. If it is update the
local dict and at the end return the game id with local dict with max values of
RGB as an array.
Not pretty because of lots of manual indexing. But effective. The result seems to be right.
Now we know the maximum colored cubes count, we can use reject: to remove
anything if it exceeds the official limit:
((((gamesCollection collect: [ :each | maxRGBinSingleGame value: each ])
reject: [ :each | ((each at: 2) at: (Color named: 'red')) > 12 ])
reject: [ :each | ((each at: 2) at: (Color named: 'green')) > 13 ])
reject: [ :each | ((each at: 2) at: (Color named: 'blue')) > 14 ])
This correctly gets rid of game 3 and 4.
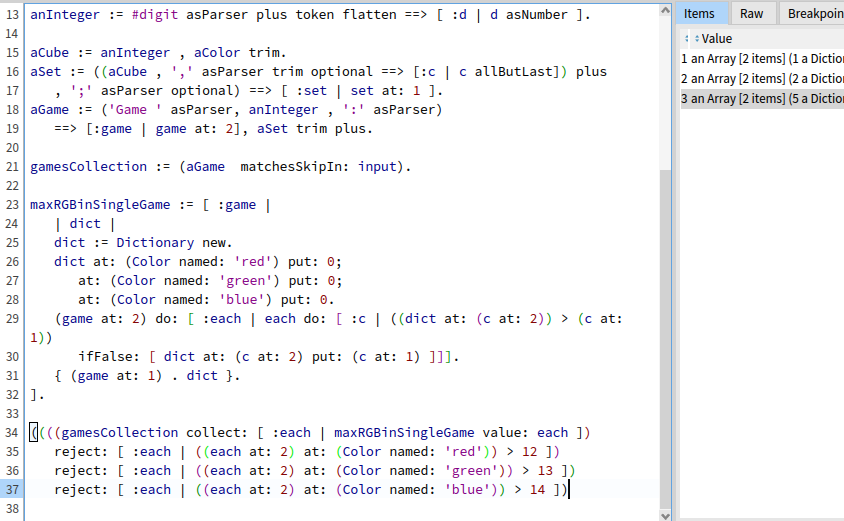
Now fold the ids using inject:into: and we get the correct result 8.
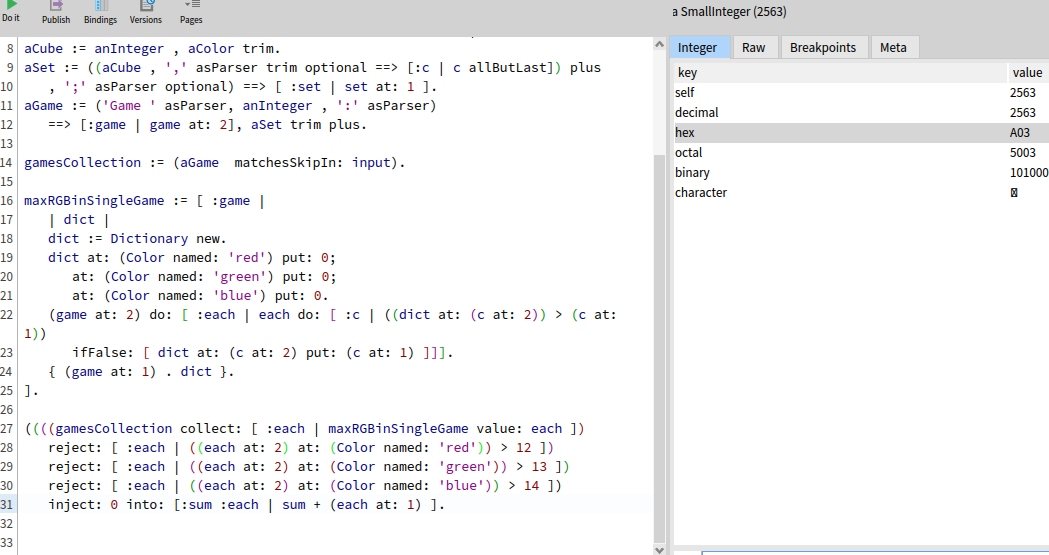
((((gamesCollection collect: [ :each | maxRGBinSingleGame value: each ])
reject: [ :each | ((each at: 2) at: (Color named: 'red')) > 12 ])
reject: [ :each | ((each at: 2) at: (Color named: 'green')) > 13 ])
reject: [ :each | ((each at: 2) at: (Color named: 'blue')) > 14 ])
inject: 0 into: [:sum :each | sum + (each at: 1) ].
changing the sample input with the actaul input.txt and submitting the
result, we pass the part 1 of the puzzle.
Day 2 - part 2
part 2 turned out to be simple. We need to again calculate the
maxRGBinSingleGame (though they worded it differently) but this time we have
to multiply each max r g b value in a game and sum the result.
Everything up until maxRGBinSingleGame remains untouched, only the last step
needs to be changed.
((gamesCollection collect: [ :each | maxRGBinSingleGame value: each ])
collect: [ :each | ((each at: 2) values) inject: 1 into:[:prod :e| prod * e
]]) inject: 0 into: [ :sum :e | sum + e ].
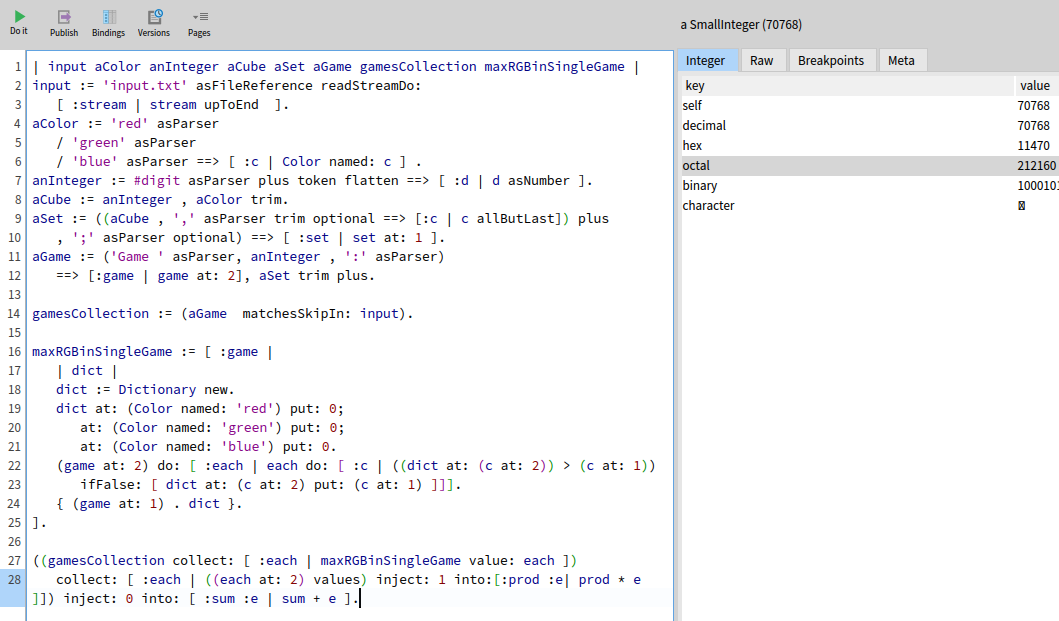
and the answer is accepted. This concludes today’s puzzle.
Thanks for reading.