Advent of Code 2023 Using Pharo Smalltalk Day 3
This was a busy week and I was unable to make a single post throughout the week. This however, does not mean I have abandoned AoC. I will try to catch up but I should mention that finishing everyday was not the goal to begin with, the goal for me is to learn Pharo while doing as many puzzles as I can.
Part 1
Sample input for part 1 is :
467..114..
...*......
..35..633.
......#...
617*......
.....+.58.
..592.....
......755.
...$.*....
.664.598..
If a number is surrounded by . alone (including diagonally), then it is
invalid and we have to reject it. After that the sum of remaining valid numbers
is the answer. In the sample 114 and 58 are invalid.
Let's open playground in pharo and insert the input :
| input |
input := '467..114..
...*......
..35..633.
......#...
617*......
.....+.58.
..592.....
......755.
...$.*....
.664.598..' lines.
I am also seprating the lines with lines message to string (In day 1 and 2, I
was manually calling splitOn with newline to do that 🤦♂️).
Now we need to calculate neighbors for each number. But before we do that, we
need to make sure that every number has 8 neighbors, right now, the cell at
corner will have only 3 neighbors, cell at edge will have 5 corners and so on.
One trick I learned some time ago while doing TicTacToe was to surround the
input with one additional . on all sides, which greatly simplifies
calculations because now every cell (characters in this case) that we care about
will have 8 neighbors.
Also, I will not show the declaration of variables from now on. At the end I will link the complete source.
padLines := [ :col |
| paddedlineSize padLine result|
paddedlineSize := (col first) size + 2.
padLine := '.' repeat: paddedlineSize .
result := col collect: [ :each | '.',each,'.'].
result addFirst: padLine.
result addLast: padLine ;
yourself.
].
paddedLines := (padLines value: input asOrderedCollection).
We add a line of dots at the start and at the end, while also adding a single
. at the start and end of the line. since addFirst and addLast are not
defined for arrays, we pass input as OrderedCollection.
Now to detect numbers, we will use PetitParser.
aNumber := #digit asParser plus.
numberRanges := paddedLines collect: [:each | aNumber matchingSkipRangesIn: each ].
We are using matchingSkipRangesIn:, which doesn't directly gives the matching
number but the number's range in the string.
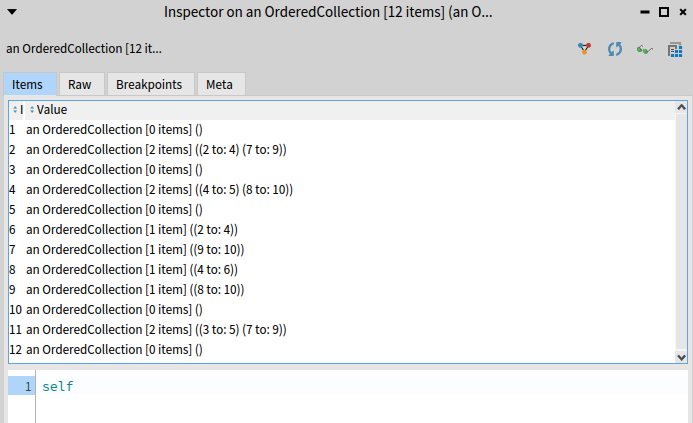
So the first line doesn't have any number, because we added a line of dots. In
second line, (2 to: 4) is the number 467. It starts at 2 because we
added a . at the start of the line.
generateNeighbors := [ :numInterval :line |
| currentLine previousLine nextLine start end result number |
previousLine := paddedLines at: (line - 1).
currentLine := paddedLines at: line.
nextLine := paddedLines at: (line + 1).
start := (numInterval first) - 1.
end := (numInterval last) + 1.
number := (currentLine copyFrom: (numInterval first)
to: (numInterval last)) asNumber .
result := (previousLine copyFrom: start to: end),
(currentLine at: start) asString ,
(nextLine copyFrom: start to: end ),
(currentLine at: end) asString.
{ number . result}
].
numbers := OrderedCollection new.
numberRanges doWithIndex: [ :each :index |
each isNotEmpty
ifTrue: [numbers add: (each collect: [ :n |
(generateNeighbors value: n value: index)])]].
numbers
which gives:
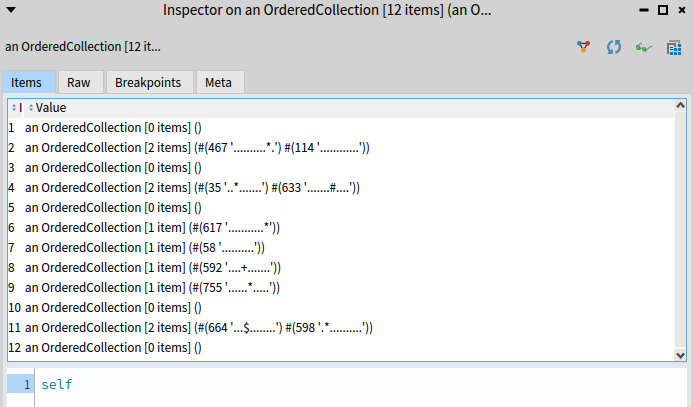
Now any pair that has only . as neighbors is rejected and we sum the rest:
((numbers collect: [ :each |
each reject: [ :e | (e at: 2) matchesRegex: '\.*']
thenCollect: [ :e | e at: 1 ]]) flattened)
inject: 0 into: [ :sum :e | sum + e ]
Replace the sample input with the real input and the part 1 is complete.
Part 2
In part 2, we need to find pair of numbers which share the same * as neighbor.
Then we need to multiply those pair of numbers and add them all. It was easy
enough to do this for sample input, but the real input has some edge cases which
were harder to find. That is when I decided to represent the input as 2D grid
and visualize it with Roassal.
I found a 2D grid implementation on github, so we can use that. Evaluating the following should load it.
Metacello new
baseline: 'ContainersGrid';
repository: 'github://Ducasse/Containers-Grid/src';
load.
The package provides a CTGrid class which we are going to subclass, because we
will add some additional methods to it. Add a new class in your package named
Grid2D which subclasses CTGrid. The code at this point looks like:
| input padLines paddedLines grid |
input := '467..114..
...*......
..35..633.
......#...
617*......
.....+.58.
..592.....
......755.
...$.*....
.664.598..' lines.
padLines := [ :col |
| paddedlineSize padLine result|
paddedlineSize := (col first) size + 2.
padLine := '.' repeat: paddedlineSize .
result := col collect: [ :each | '.',each,'.'].
result addFirst: padLine.
result addLast: padLine ;
yourself.
].
paddedLines := padLines value: input asOrderedCollection.
grid := Grid2D columns: ((paddedLines at: 1) size) rows: (paddedLines size).
paddedLines doWithIndex: [ :each :row |
each doWithIndex: [ :e :col |
grid atRow: row atColumn: col put: e] ].
We pad the lines as we did in part 1, then initialize a grid with the data. The grid in the inspector looks like:
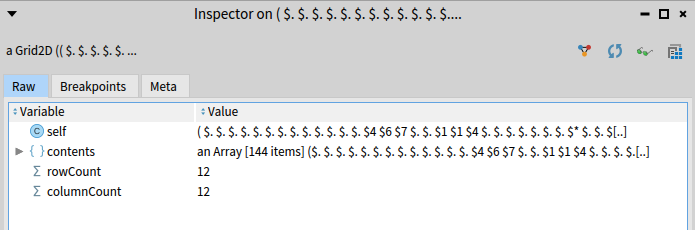
That's not how a grid should look. This is where Roassal comes in. Use the main
menu Library > Roassal3 > Load > Load full version to load Roassal. Then add a
method visualize to our Grid2D class. The actual name of the method could be
anything, what matters is that it returns an instance of RCanvas's canvas.
visualize
| c |
c := RSCanvas new.
self withIndicesDo: [ :each :row :col |
| circle labeledCircle |
circle := RSCircle new size: 30.
circle @ (RSPopup new
text: [ :e | row@col];
yourself).
circle color: Color pink muchLighter.
labeledCircle := { circle . RSLabel new color: Color black; text: each }
asGroup asShapeFor: each.
c add: labeledCircle ].
RSGridLayout new lineItemsCount: self rowCount ; on: c shapes.
c @ RSCanvasController.
^ c canvas
This gives a much better result. The output is interactive and we could zoom and pan around.
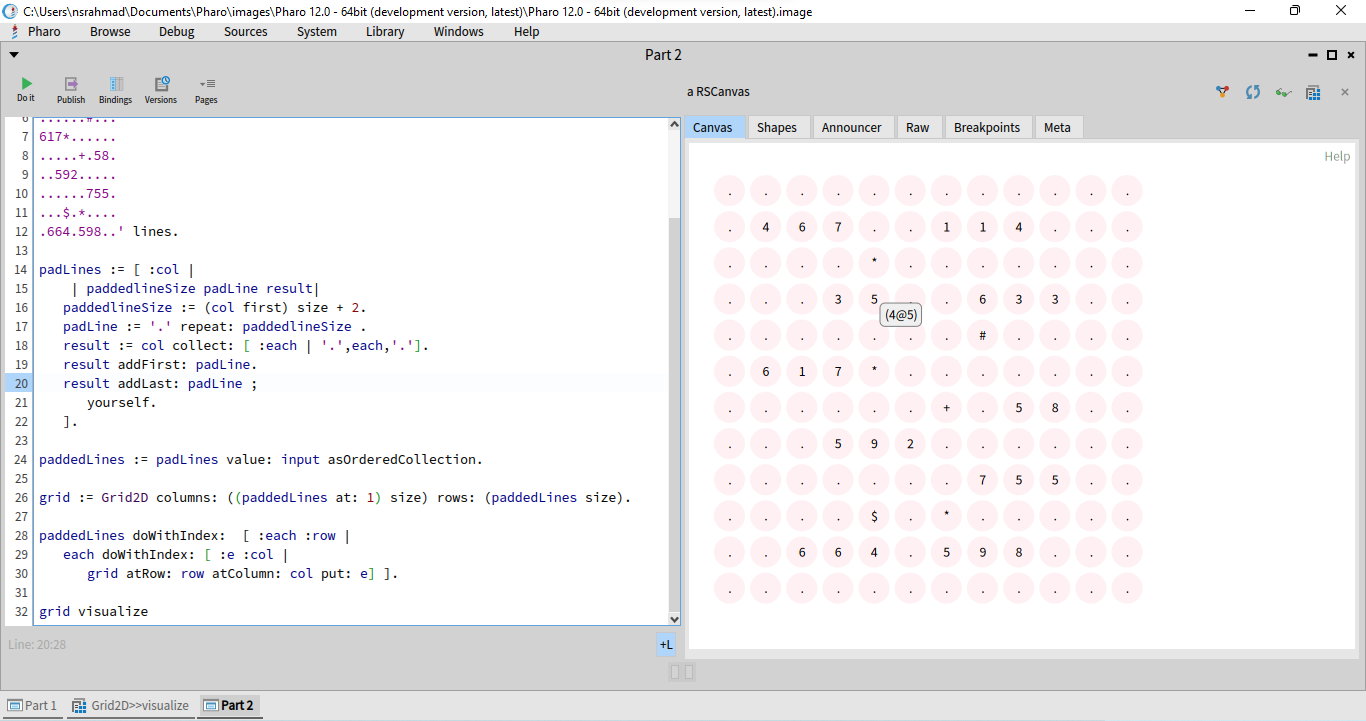
We could do better, let's add another method visualizeWithHighlight to
Grid2D:
visualizeWithHighlight: aBlock
| c |
c := RSCanvas new.
self withIndicesDo: [ :each :row :col |
| circle labeledCircle |
circle := RSCircle new size: 30.
circle @ (RSPopup new
text: [ :e | row@col];
yourself).
circle color: (aBlock value: each).
labeledCircle := { circle . RSLabel new color: Color black; text: each }
asGroup asShapeFor: each.
c add: labeledCircle ].
RSGridLayout new lineItemsCount: self rowCount ; on: c shapes.
c @ RSCanvasController.
^ c canvas
Everything is same except we pass a block which sets the color of the circle.
This lets the caller decide which color to use for each circle. For example, if
we wanted to highlight each * on the grid, we could do:
grid visualizeWithHighlight: [ :each | each = $*
ifTrue: [ Color pink ]
ifFalse: [ Color pink muchLighter ] ].
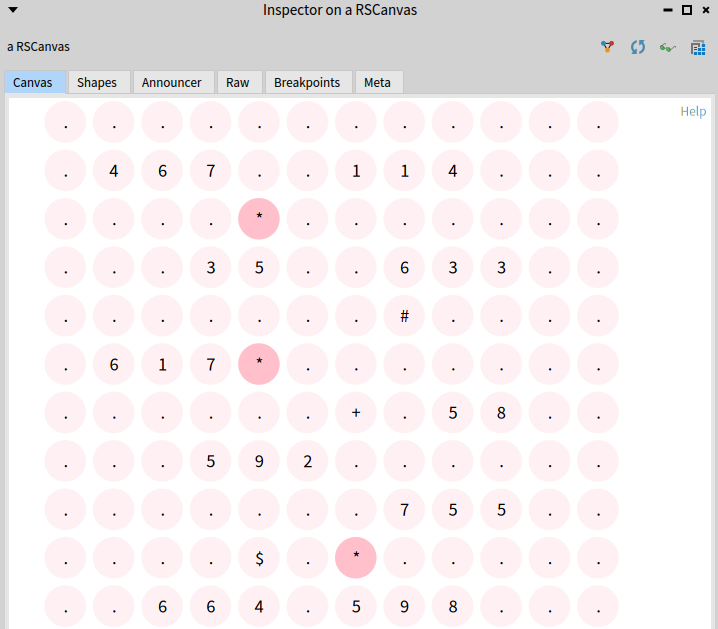
If we change the highlight color to red and switch input with real input, then
the *'s on real input looks like:
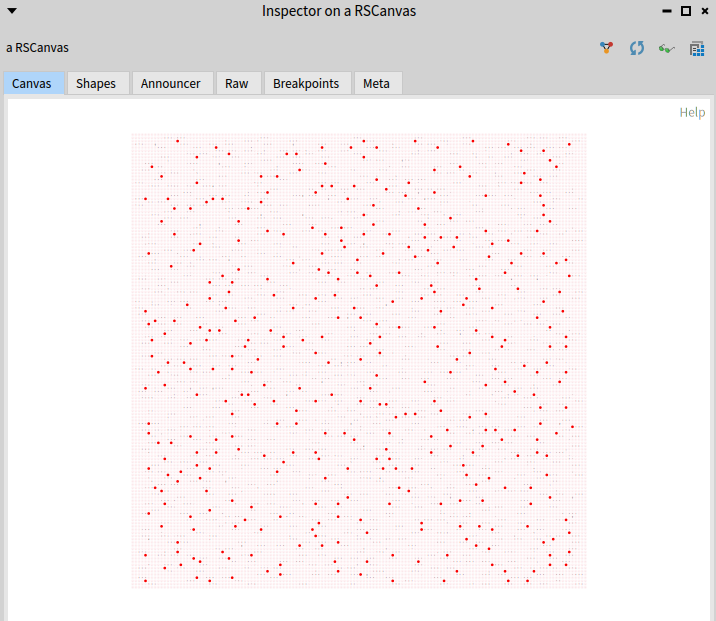
You can zoom in and out and pan as usual. Mouse over gives me the actual location of the cell.
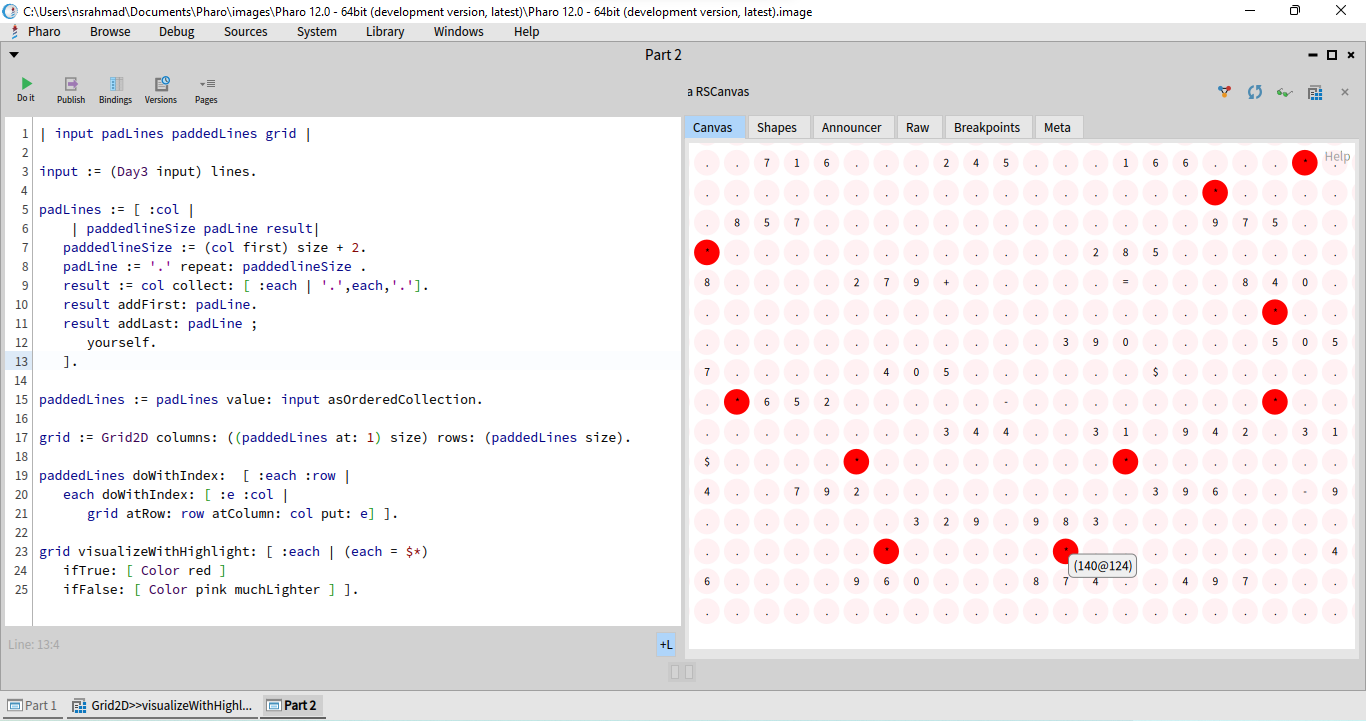
Also added a at: method to Grid2D which takes a point like 1@1 and gives
us the item there:
at: aPoint
aPoint isPoint ifTrue: [^ self atRow: aPoint x atColumn: aPoint y ].
^ self contents at: aPoint
Enough about visualization, let's get back to the puzzle.
First helper function we need is called readNumberAt. Given a point on the
grid with a digit, This function returns the whole number by combining
consecutive digits on the left or right.
readNumberAt := [ :pos :aGrid |
| result lPos rPos |
lPos := pos - (0 @ 1).
rPos := pos + (0 @ 1).
result := ''.
[(aGrid at: pos) isDigit & ((aGrid at: lPos) isDigit)] whileTrue:
[result := (aGrid at: lPos) asString , result.
lPos := lPos - (0 @ 1)].
(aGrid at: pos) isDigit ifTrue:
[result := result , (aGrid at: pos) asString].
[(aGrid at: pos) isDigit & (aGrid at: rPos) isDigit] whileTrue:
[result := result , (aGrid at: rPos) asString.
rPos := rPos + (0 @ 1)].
result
].
Another helper is a neighbors fucntion, which gives eight neighbors of a point
on grid. I am aware of the eightNeighbors method of the Point class which is
part of the standard library. But it is problemetic for us, because it starts
from the point directly below and goes anticlockwise. If a 2 digit number is at
our lower left side, then the digtis will get split up. We don't want that,
hence our own neighbors function. It starts from upper left corner and goes
clockwise:
neighbors := [ :aPoint |
{ {aPoint + (-1 @ -1) . aPoint + (-1 @ 0) . aPoint + (-1 @ 1)}
. aPoint + (0 @ 1) . {aPoint + (1 @ 1) . aPoint + (1 @ 0)
. aPoint + (1 @ -1) }. aPoint + (0 @ -1) } ].
We go around the grid and collect each star's location:
stars := OrderedCollection new.
grid withIndicesDo: [ :each :row :col |
(each = $*) ifTrue: [stars add: row@col]].
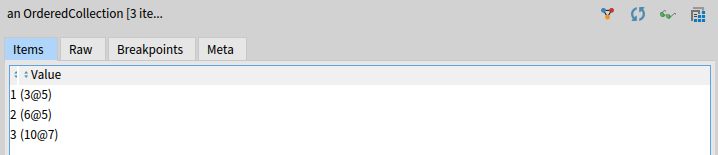
Then we go around each star and collect numbers which are in their neighborhood:
starsWithNumbers := (stars collect: [ :each | neighbors value: each])
collect: [:e |
{ (e at: 1) collect: [:top | readNumberAt value: top value: grid]
. readNumberAt value: (e at: 2) value: grid
. (e at: 3) collect: [:bottom | readNumberAt value: bottom value: grid]
. readNumberAt value: (e at: 4) value: grid} flattened].
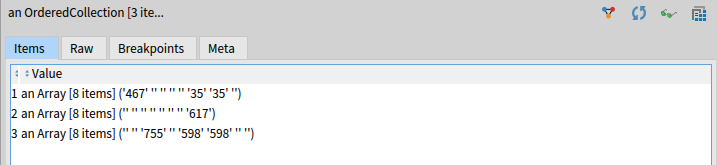
Notice how if 2 digits are neighbors of * then they get collected twice.
Luckily they will always be adjacent so getting rid of them is not that hard.
The naive version, by using asSet gets in trouble because one of the pairs are
same numbers, and they are both at the top too. But the distinguishing factor
is, they will have a space between them as a ..
starsWithNumbers := starsWithNumbers collect: [ :each |
| result |
result := OrderedCollection new.
each do: [ :x |
result isEmpty ifTrue: [ result add: x]
ifFalse: [(result last) = x ifFalse: [result add: x]]].
result].
This gets rid of the duplicates but keeps the same numbers if they appear as pair.
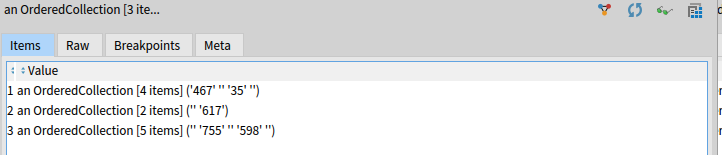
Now we need to get rid of blanks and the stars with single number as neighbor:
starsWithNumbers := (starsWithNumbers collect: [ :each |
each reject: [ :e | e = '' ]
thenCollect: [:e | e asNumber]])
select: [ :e | (e size) > 1 ].
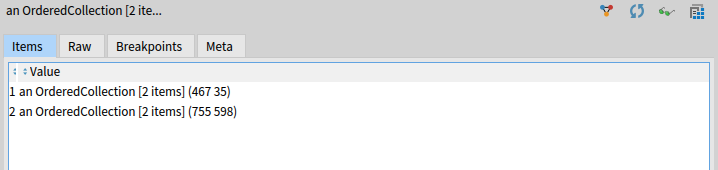
The data is finally in the desired shape. Reduce them with:
starsWithNumbers inject: 0 into: [ :sum :e | ((e at: 1) * (e at: 2)) + sum ].
And we are finished. The source is at the repository available at https://github.com/nsrahmad/AdventOfCode2023 .
This was harder than usual because how useless the sample input was. Every edge case was in the actual input rather than in the sample. I really hated that at first but after finishing it, It didn't feel that bad after all.
Reminds me of my favorite quote from "Ender's Game" by Orson Scott Card:
“In the moment when I truly understand my enemy, understand him well enough to defeat him, then in that very moment I also love him. I think it’s impossible to really understand somebody, what they want, what they believe, and not love them the way they love themselves. And then, in that very moment when I love them.... I destroy them.”
I guess it is also true of software bugs and hard puzzles. See you soon.